CHAPTER 24, Inc., MADISON, WI
SBE 24 GeoSat Pt2

GEOSTATIONARY ORBITS PART 2:
ORBITAL GEOMETRY

by Neal McLain, CSBE
Copyright © 1995-2002 by Neal McLain

This is the second in a series of articles about geostationary orbits; i.e., the orbits occupied by communications satellites which remain at fixed points in the sky. In this series, we cover basic physical principles, orbital geometry, pointing angles, and antenna mounts.

This second article describes the geometry of the geostationary orbit.

THE GEOSYNCHRONOUS ORBIT

In Part 1, we defined a geosynchronous orbit as follows:

• ORBIT PERIOD: One sidereal day, or about 23 hours 56 minutes 4 seconds. During one sidereal day, the earth rotates about its polar axis exactly once. To be geosynchronous, a satellite must orbit the earth in exactly the same time period.

• AVERAGE ORBIT RADIUS: 42,155 Km. We calculated this value from Kepler's Third Law. We then subtracted the earth's radius (6370 Km) from the orbit radius to determine the orbit height above the earth: 35,785 Km., or about 22,236 miles.

Note that this definition doesn't say anything about the shape of the orbit, or the orientation of the orbit plane with respect to the equator. The orbit can be highly elliptical, and/or it can be inclined with respect to the equator, and still be synchronous with the Earth's rotation.

THE GEOSTATIONARY ORBIT

In this series of articles, we're interested in a special kind of geosynchronous orbit called a geostationary orbit. A satellite moving in a geostationary orbit remains at a fixed point in the sky at all times. This, of course, is desirable for radio communications because it allows the use fixed antennas.

To be geostationary, the orbit must meet three criteria:

• The orbit must be geosynchronous.

• The orbit must be a circle.

• The orbit must lie in the earth's equatorial plane.

The following figure illustrates the geostationary orbit. Note that individual satellites within the orbit are identified by longitudinal position east or west of the Prime Meridian.

All geostationary orbits comply with the following:

PARAMETER METRIC UNITS U.S. UNITS
 Height above equator 35,785 Km  22,236 Miles 
 Average Orbit Radius 42,155 Km  26,194 Miles 
 Orbit Circumference 264,869 Km  164,581 Miles 
 Arc length per degree 736 Km  457 Miles 
 Orbital Velocity 11,066 Km / hr  6,876 Miles / hr 
Source: Computations by the author, based on data taken from Astronomy Data Book
by J. Hedley Robinson (New York: John Wiley & Sons, 1972).

To understand the importance of these criteria, consider the result if the orbit fails to meet them.

• If the orbit is not geosynchronous, the satellite does not move at the same rate as the earth's rotation. Thus, from the point of view of an observer on earth, the satellite appears to be in continuous motion, and it periodically disappears below the horizon.

• If the orbit is not a circle, the satellite does not move at constant velocity (Kepler's Second Law). Instead, it appears to oscillate east-and-west at a rate of two cycles per sidereal day.

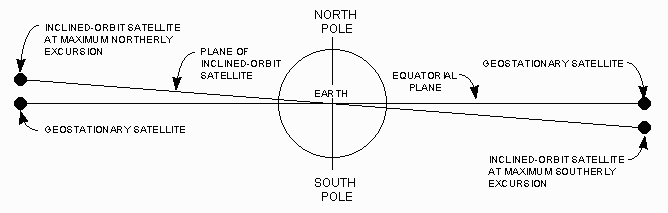
• If the orbit does not lie in the equatorial plane, the satellite does not remain at a fixed point in the sky. Instead, it appears to oscillate north-and-south at a rate of one cycle per sidereal day. The following figure illustrates this situation. Note that during the course of one orbit around the earth (one sidereal day), the satellite moves from MAXIMUM NORTHERLY EXCURSION (left side of the illustration) to MAXIMUM SOUTHERLY EXCURSION (right side) and back to MAXIMUM NORTHERLY EXCURSION.

Note that the terms geosynchronous and geostationary are not synonymous: geosynchronous specifies only the orbit period, but geostationary also specifies the shape and orientation of the orbit.

These definitions are consistent with the definitions used by the United States Federal Communications Commission (FCC). The following definitions are quoted from the FCC rules, as published in Title 47, Section 2.1, of the United States Code of Federal Regulations:

• Geosynchronous Satellite. An Earth satellite whose period of revolution is equal to the period of rotation of the Earth about its axis.

• Geostationary Satellite. A geosynchronous satellite whose circular and direct orbit lies in the plane of the earth's equator and which thus remains fixed relative to the earth; by extension, a satellite which remains approximately fixed relative to the earth.

These FCC definitions are based on definitions specified in international agreements to which the United States is a signatory.

THE CLARKE BELT

The circular belt containing all geostationary orbits is called the Clarke Belt, in honor of Arthur C. Clarke (1917-       ), British physicist and astronomer who first published the concept of "stationary orbits."

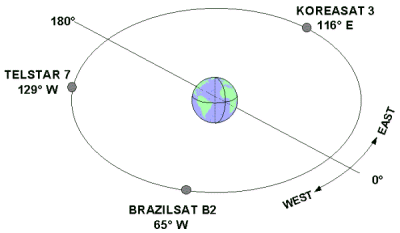
Specific satellite positions in the Clarke Belt are identified by longitude (or, more precisely, by the longitude of the point on the equator directly beneath the satellite). The following figure shows examples of three satellites in the Clarke Belt:

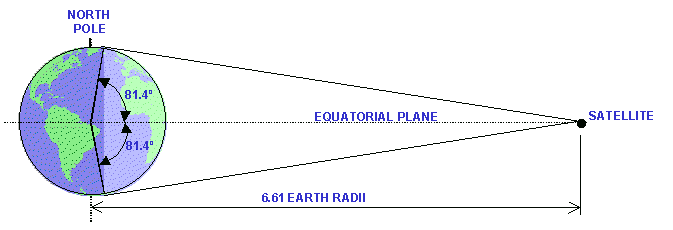
The signal from one geostationary satellite covers about 40% of the earth's surface:

At the equator, a 162°-segment of the Clarke Belt is visible. The visible segment becomes smaller as the latitude increases, and becomes zero at latitude 81.4°. North of 81.4° north latitude (and south of 81.4° south latitude), the entire Clarke Belt is hidden below the horizon.

Theoretically, only four or five satellites would be needed to cover the entire land area of the earth between 81° north latitude and 81° south latitude. Indeed, Clarke's original concept for "stationary orbits" contemplated only three such satellites, spaced 120° apart.

In fact, dozens of satellites have been deployed along the Clarke Belt in order to accommodate the ever-growing demand for communications channels. In many parts of the Clarke Belt, adjacent satellites using the same frequency band are located within 2° of each other.

AN EARTHLING'S VIEW OF THE CLARKE BELT

Imagine an observer standing at an earth station site at latitude 45°, looking south (or, in the case of the observer in the Southern Hemisphere, looking north):

Now imagine two large arches in the sky. The following figure shows how these arches would look to our observer:

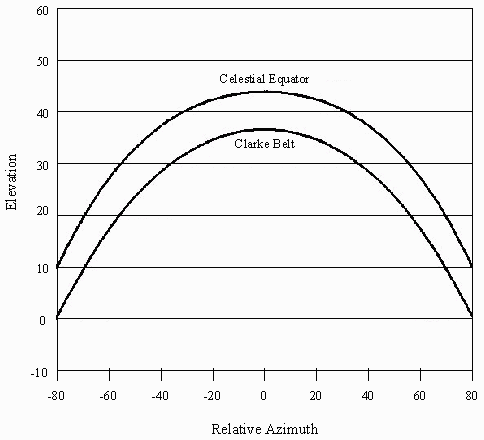In this figure:

• The horizontal line at 0° represents the horizon. It is marked in degrees of relative azimuth; i.e., the angle, in degrees, east or west of the point directly south (or north) of the earth station.

• The vertical axis represents height, or elevation, relative to the horizon, in degrees. Points below the horizon are, of course, not visible to our observer.

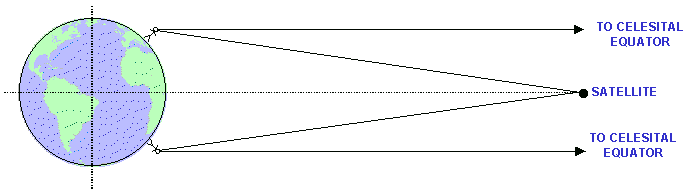
These two large arches are the Celestial Equator and the Clarke Belt:

• The Celestial Equator is a circle, at an infinite distance from the earth, lying in the earth's equatorial plane.

• The Clarke Belt is also a circle lying in the earth's equatorial plane; however, because it is nearer to the earth than infinity, it appears to lie below the Celestial Equator.

• The highest point in the each arch is called the peak; it is located directly south (or north) of the observer, along the same meridian as the observer.

The appearance of these two arches varies dramatically as a function of the observer's latitude. The following figures show the arches for six different latitudes, from the equator to the North (or South) Pole.

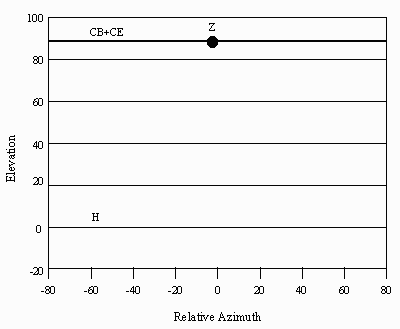
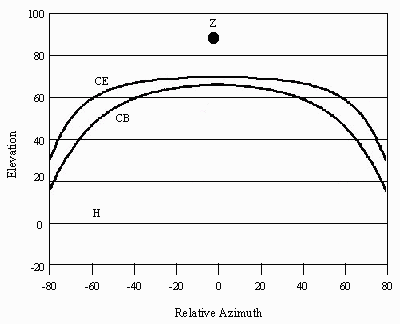
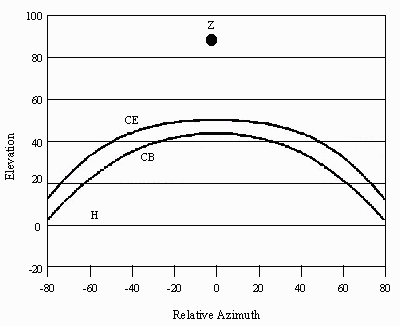
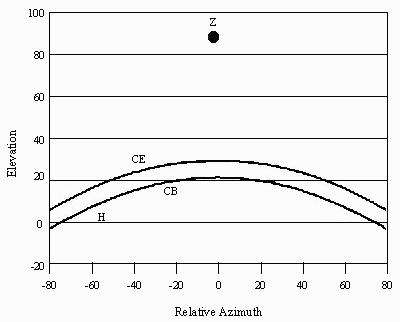
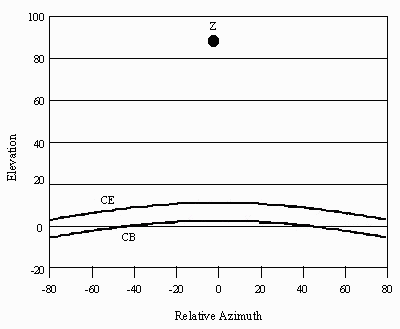
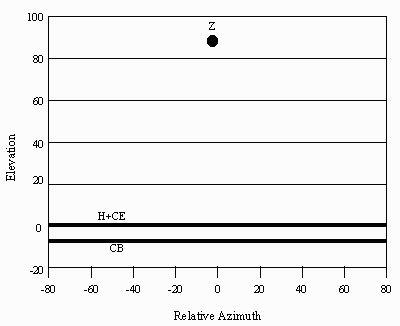
Abbreviations: CB = Clarke Belt; CE = Celestial Equator; H = Horizon; Z = Zenith.

• Latitude 0°. At the equator, the Clarke Belt and the Celestial equator merge together into a single line running from east to west. Peak elevation is at the zenith, the point directly overhead.

• Latitude 20°. The peak elevation of the Celestial Equator falls at 70° above the horizon.


• Latitude 40°. The peak elevation of the Celestial Equator falls at 50° above the horizon.

• Latitude 60°. The peak elevation of the Celestial Equator falls at 30° above the horizon. Note that the sum of peak elevation of the Celestial Equator plus latitude always equals 90°.


• Latitude 80°. At this latitude, the Clarke Belt almost disappears: a narrow segment is just visible above the horizon.


• Latitude 90°. At the pole, the entire Clarke Belt disappears below the horizon. The Celestial Equator coincides with the horizon in all directions.


POINTING ANGLES

Since all geostationary orbits fall in the Clarke Belt, each geostationary satellite can be represented as a point in the lower arch. Each point in this arch can be uniquely specified by the two parameters azimuth and elevation.

These parameters are called pointing angles. In the next article, we'll discuss pointing angles in detail.

CONTINUE TO PART 3 - POINTING ANGLES
Orbits Index Page
Top of Page