
|
|
 CHAPTER 24, Inc., MADISON, WI |
- Home
- Meetings
Schedule - Meeting
Minutes - Chapter
By Laws - Chapter
Officers -
Technical
Documents -
EAS
Info -
Chapter
Archives - Sustaining
Members -
Broadcasters
Clinic - DTV for
Consumers - Links
GEOSTATIONARY ORBITS PART 5: by Neal McLain, CSBE |
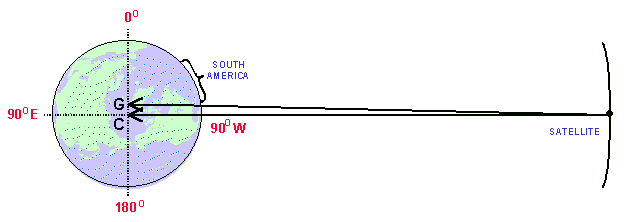 |
A satellite at 90° west longitude. Point C = geometric center. Point G = apparent center of gravity.
Point G lies east of Point C because of the land mass of South America. Note that the vector
to the earth's apparent center of gravity (Point G) is not congruent with the vector to
the earth's geometric center (Point C). In the case of geostationary satellites visible from
North America, the land mass of South America tends to cause them to drift to the east.
ROCKETS
To counteract these forces, the satellite must be fitted with some mechanism to move the satellite back into position when it drifts. In outer space, only one such mechanism is available: the rocket.
Now, let's stop and discuss rockets. The popular conception of a rocket is something very large which burns some sort of fuel to produce an enormous thrust.
More generally, a rocket is any device which produces a force by ejecting mass. Fuel-burning rockets produce force by ejecting the products of combustion. But combustion isn't necessary: any mechanism for ejecting mass will produce a force. A common example: a loose balloon flying around the room ejecting its air supply.
The direction of the force produced by a rocket is equal and opposite to the force required to eject the mass. This, of course, is Newton's Third Law: for every force, there is an equal and opposite reaction force.
STATIONKEEPING
Communications satellites are fitted with small rockets called thrusters. On command from the a control station, a thruster is fired; during the firing, it ejects a gas called
fuel or propellant. Like the air escaping from the balloon, the ejected gas produces the force.
A ground control station precisely controls all parameters involved in a firing: the position of each thruster relative to the satellite, the timing and duration of each fire, and the pressure
of the ejected propellant. If these parameters are controlled properly, the satellite can be maintained at proper position and attitude for years.
This process is called stationkeeping.
SATELLITE LIFE EXPECTANCY
Every time a thruster is fired, propellant is used. Once the supply of propellant is exhausted, the satellite cannot be maintained at proper position and attitude, and the satellite must be
retired. Propellant capacity is the primary factor which determines the useful life of a communications satellite.
It is easy to understand that a primary goal of every satellite owner is the conservation of propellant. Many computer studies have been done to determine the optimum trade-off between
satellite stability and propellant usage.
These studies have shown that a substantial majority of the propellant is used for just one stationkeeping function: keeping the satellite from drifting along its north-south axis. Kent Carson, director of advanced programs for Comsat Systems Division, has stated that between 80% and 90% of the propellant is used for this function alone. [1]
INCLINED ORBITS
Let us now consider what happens if the owner of a satellite simply stops north-south stationkeeping, and lets the satellite drift freely along its north-south axis.
Two things happen.
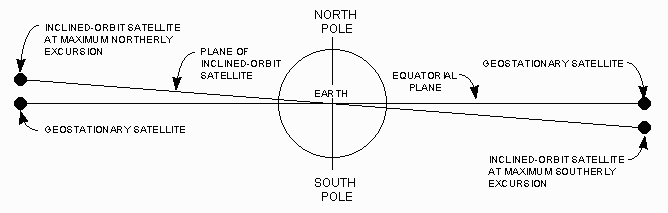 |
From a point on the earth's surface, the satellite appears to oscillate along its north-south axis at a rate of one cycle per sidereal day.
• Secondly, for reasons beyond the scope of this article (conservation of angular momentum), the orbit assumes a slightly elliptical shape. As a result, the satellite no longer moves at constant velocity (Kepler's Second Law). From a point on the earth's surface, it appears to oscillate along its east-west axis at a rate of two cycles per sidereal day.
• The orbit assumes a slightly elliptical shape; therefore, the satellite appears to oscillate along its east-west axis at a rate of two cycles per sidereal day.
The following figure illustrates this pattern for GStar 3, as it appeared from Madison, Wisconsin (about 43° north latitude) during November, 1995:
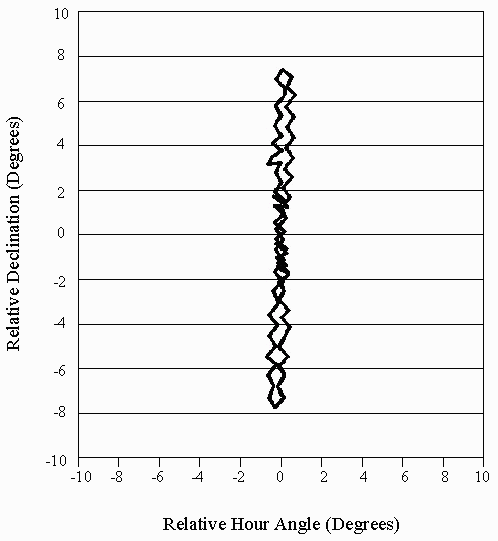 |
Data plot prepared by the author using Borland Quattro data presentation software.
Original data courtesy of Communication Technologies, Inc.
The original data for this plot consists of 78 data points representing tracking activity for one sidereal day.
Each data point represents the position of the antenna after peaking.
The center of the figure-8 pattern (Point 0,0) represents the original geostationary position of GSTar 3 before it was allowed to drift freely along its north-south axis.
Horizontal axis is hour angle, in degrees, relative to Point 0,0.
Vertical axis is declination, in degrees, relative to Point 0,0.
ECONOMICS
From the point of view of a satellite owner, the economics of this situation are compelling. On one hand, the revenue derived from leasing transponder time on an inclined-orbit satellite is
considerably less than the revenue which could be realized from a truly geostationary satellite. On the other hand, propellent usage is cut dramatically, thereby extending the useful life of
the satellite, often by several years. The potential revenue to be derived from this extended life more than offsets the revenue lost through reduced transponder pricing.
It comes as no surprise, then, that many satellite owners have allowed their geostationary satellites to drift into inclined orbits.
BUT IS IT GEOSTATIONARY?
Is an inclined-orbit satellite still "geostationary"?Strictly speaking, no. In Part 2, we defined geostationary as follows:
• The orbit must be a circle.
• The orbit must lie in the earth's equatorial plane. An inclined orbit is indeed geosynchronous, but it is not a circle and it does not lie in the earth's equatorial plane.
Geostationary Satellite. A geosynchronous satellite
whose circular and direct orbit lies in the plane of
the earth's equator and which thus remains fixed relative
to the earth; by extension, a satellite which remains
approximately fixed relative to the earth. [2]
An inclined-orbit satellite meets the "by extension" part of this definition as long as it is maintained in the correct east-west position (to avoid interference to adjacent satellites) and at the proper attitude (to keep the antennas aimed correctly).TRACKING
An inclined-orbit satellite poses a problem for the end user: the earth station antenna must track the satellite. For this purpose, the antenna must be equipped with a dual-axis steerable mount and a tracking controller.A dual-axis steerable mount is a motorized mount which can be moved independently about two axes: east-west and up-down. Any of the following mount types can be used:
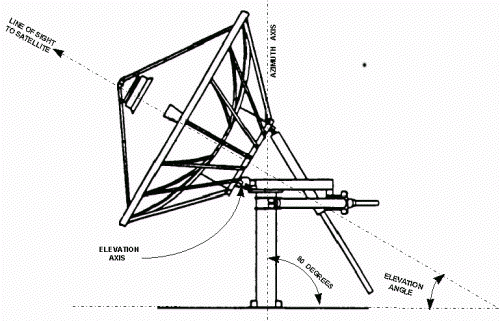 Antenna with EL/AZ-Mount (Andrew Corporation) |
• Polar mount. A polar mount can be used for tracking if it is equipped to allow adjustment about the declination axis throughout the full range of the satellite's figure-8 pattern. Example:
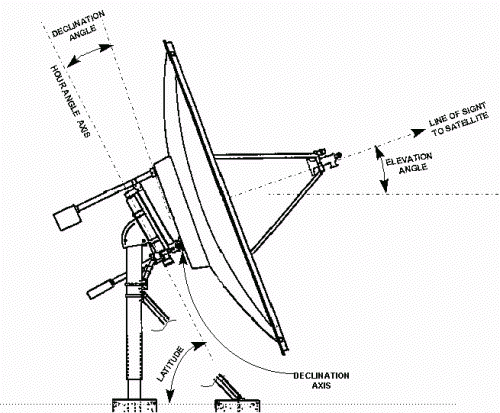 Antenna with Dual-Axis Polar Mount (Comtech Antenna Systems, Inc.) |
• Hybrid mount. Andrew manufactures a dual-axis mount which is neither EL/AZ nor polar. The up-down axis is elevation; the east-west axis falls between azimuth and hour angle.
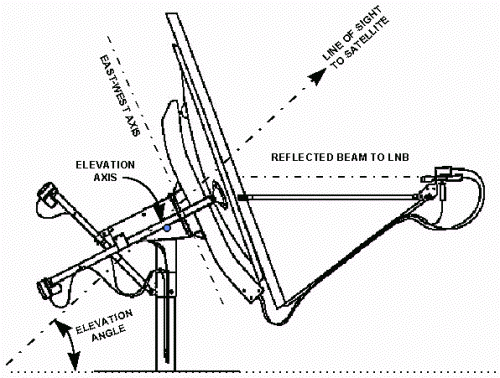 Antenna with Dual-Axis Hybrid-Mount (Andrew Corporation) |
Most AGC-controlled controllers are equipped to maintain a "history," or " map," of the figure-8 pattern. The history is established during the first day's operation; thereafter, the history is used in two ways: it tells the controller which way to move the antenna when peaking the signal, and it allows the controller to continue tracking if the satellite signal fails.
The controller updates the history during the course of normal tracking. Thus, it responds automatically to changes in the shape of the tracking-8 pattern as the satellite continues to drift along its north-south axis.
AGC-controlled controllers move the antenna in a series of short steps. For this reason, they are sometimes called "step-track" controllers. The original data used to generate the Figure-8 pattern illustrated above was produced by an AGC-controlled controller. Note that the individual steps are clearly evident in this illustration.
• Program-controlled. This type of controller mathematically calculates the pointing angles to the satellite and moves the antenna accordingly. Calculations are based on program data entered into the controller.
This type of controller is capable of moving the antenna continuously, rather than in a series of steps. This technique is advantageous in low-signal situations where any change in AGC voltage would result in degraded signal quality.
Because this type of controller calculates pointing angles from program data, it does not respond automatically to changes in the tracking pattern as the satellite drifts. For this reason, the program data must be updated periodically.
In order for this type of controller to operate satisfactorily, the program data must specify the precise position of the satellite in space at any given time and date. The position is defined in terms of six parameters called Orbital Elements (sometimes called Keplerian Elements). There are several standardized formats for specifying orbital elements; the most common is called a Two-Line Element (TLE) Data Set. TLE data sets are maintained by several of organizations, and are available from a number of websites. [3] The functions of a tracking controller can be integrated into a general-purpose antenna controller. This type of controller can move the antenna to any satellite, geostationary or inclined. When moved to an inclined-orbit satellite, the satellite is located by reference to the history or program data.
-------------------------References:
[1] Scott Chase. "Earth Station Technology: Keeping Up with Orbital Capabilities." Via Satellite Return to text.
[2] Code of Federal Regulations, Title 47, Section 2.1. Washington: United States National Archives and Records Administration. Return to text.
[3] Sources for TLE data: